Bitcoin Keys and Addresses: What you need to know.

Learn Forex Trading
Digital keys play a central role in the bitcoin network because they act as proof of ownership for the digital currency, and are necessary when signing digital transactions. Public-key cryptography is the science behind the keys, the encryption process basically uses two mathematically related, but not identical, keys - a public key and a private key, and each key performs a specific function.
What’s important to understand is that these digital keys are created and managed by digital wallets. Each wallet runs a digital (public) address, similar to the beneficiary name on a traditional paper cheque. It consists of a public key (similar to a credit card number) and a private key (similar to a credit card PIN number). In the conventional, non-digital world, the safety of your underlying funds is not compromised by having the beneficiary name printed on a cheque or entering full credit card numbers when making an online purchase. Similarly with public key cryptography, the public key and digital address are shared and exposed. However the private key, is just like your PIN on a bank card, so it should never be shared. Private keys should be kept as secret and safe as PIN numbers because they authorise the spending of your money.
Private Key
A private key is a randomly generated 256-bit number. Each bit (short for binary digit) is represented by one of two binary values, a 0 or a 1.

The following is an example of a random private key as a series of 256 bits:
1110111100100011010110101010110011111001000011011001111101001010101011011101100011001001001011100100101100100101011000101110000111011001111010111001011111110000110111111001101110100011101101010000100000100101100001110011100111001011000000010011110110110010
To wrap your head around the enormous amount of possible 256-bit combinations, just think of it as approximately 1077. Now compare that to the number of the stars in the universe, which is around 1024. Pretty huge, right?
In the world of mathematics and computer science, we put 1s and 0s into groups of 4 bits, known as half bytes. Thus, if we take the above example of a private key and format it in groups of half bytes, it would look as follows:
1110 1111 0010 0011 0101 1010 1010 1100 1111 1001 0000 1101 1001 1111 0100 1010 1010 1101 1101 1000 1100 1001 0010 1110 0100 1011 0010 0101 0110 0010 1110 0001 1101 1001 1110 1011 1001 0111 1111 0000 1101 1111 1001 1011 1010 0011 1011 0101 0000 1000 0010 0101 1000 0111 0011 1001 1100 1011 0000 0001 0011 1101 1011 0010.
As there are a total of 16 possible 4-bit combinations, each half byte is made to correspond to a decimal number between 0 and 15, as per the table below:
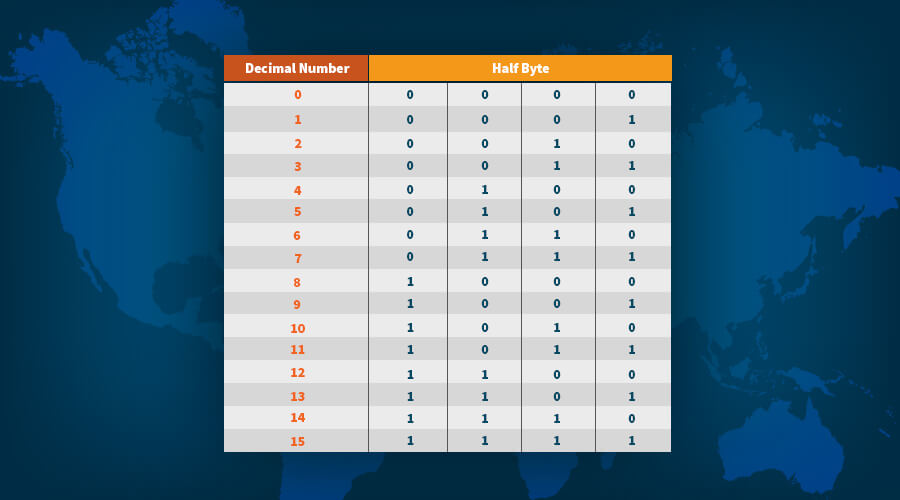
So, using the above table, we can re-write our private key example by mapping each half byte to the corresponding decimal number. The result looks like so:
14 15 2 3 5 10 10 15 12 15 9 0 13 9 15 4 10 10 13 13 8 12 9 2 14 4 11 2 5 6 2 14 1 13 9 14 11 9 7 15 0 13 15 9 11 10 3 11 5 0 8 2 5 8 7 3 12 11 0 1 3 13 11 2
Next to the binary system that has 2 digits (0 or 1), and the decimal system that consists of 10 digits from 0 to 9, there is also the hexadecimal system which consists of 16 alphanumeric characters, ordered from 0 to F. These are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, and F.
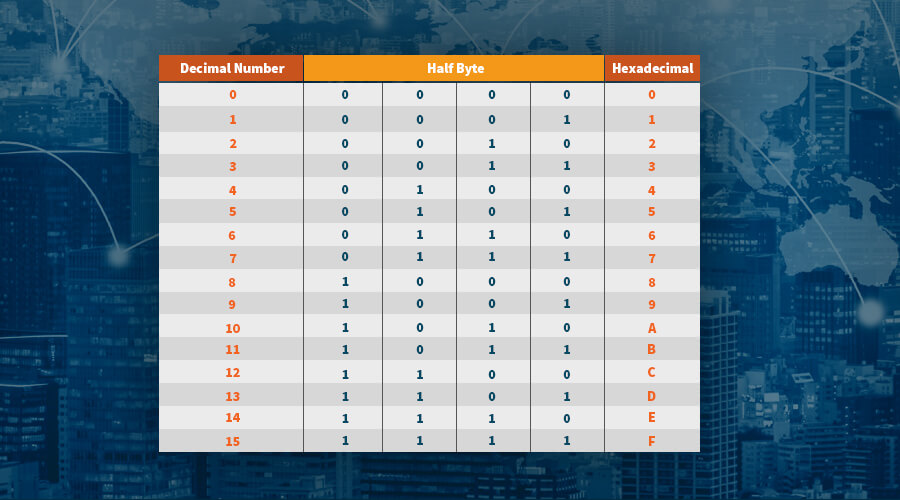
Keeping all three systems in mind, our original 256-bit private key converts to a hexadecimal number as follows:
ef235aacf90d9f4aadd8c92e4b2562e1d9eb97f0df9ba3b508258739cb013db2
Private keys appear as 51 alphanumeric characters when the so-called Base58 encoding system is used. Base58 is a binary-to-text encoding structure which includes both upper and lower case characters of the English alphabet, as well as numbers 1 to 9. In order to avoid any confusion and mistakes with similar looking characters in typing private keys, the number zero (0), the lower and upper case letter o, capital i (I) and lower case L (I), have all been omitted. Private keys encoded with the Base58 format always start with 5H, 5J or 5K. For example, 5HpHagT65TZzG1H3CSu63k8Dbpv8s5ip4nEB3kEsreAvUcVfH34
Public Keys
Public keys are created from private keys using a mathematical concept known as “elliptic curve multiplication”, which can generate a unique public key from a private key but more importantly, not the other way around. In this way, a private key is used to digitally sign (or authenticate) a transaction to spend a number of bitcoins. By publicising the signature and the public key, anyone can infer that the transaction is valid without needing to actually see the private key. In other words, they can see that:
- The transaction was indeed sent by the private key holder, i.e. the legitimate owner of the bitcoins, and
- At the time of the transaction, the owner owned the amount of bitcoins that appears on the transaction
Public keys can be either 520 bits (65 bytes) long, or 264 bits (33 bytes) long if the key is compressed.
Bitcoin Address
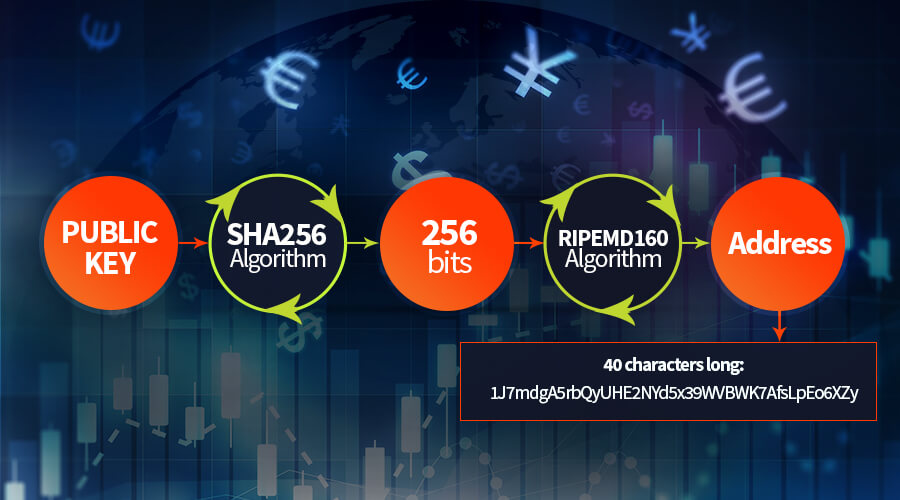
To get to the bitcoin address, the public key is fed into a cryptographic algorithm known as SHA (Secure Hash Algorithm), designed by the Unites States National Security Agency (NSA). The SHA-256 algorithm takes an input string of any size and converts it to exactly 256 bits. After this, the resulting 256-bit long string is fed again to the SHA algorithm, and more specifically to RIPEMD-160, another family of cryptographic algorithms.
The end result is a 40 characters long Bitcoin Address:
Conclusion
Public key cryptography is of paramount importance to the digital currency payment system because it is used to confirm ownership of cryptocurrencies like bitcoin. CPU power continues to improve, as does the cryptographic complexity, in order to ensure data security and transmission over an unsecure medium of communication like the Internet. Private and public keys are managed by digital wallets and are essential to the smooth operation of the bitcoin blockchain.
*Trading CFDs on Bitcoin is only available under Exinity Limited
Disclaimer: This written/visual material is comprised of personal opinions and ideas. The content should not be construed as containing any type of investment advice and/or a solicitation for any transactions. It does not imply an obligation to purchase investment services, nor does it guarantee or predict future performance. FXTM, its affiliates, agents, directors, officers or employees do not guarantee the accuracy, validity, timeliness or completeness of any information or data made available and assume no liability for any loss arising from any investment based on the same.
Risk Warning: There is a high level of risk involved with trading leveraged products such as forex and CFDs. You should not risk more than you can afford to lose, it is possible that you may lose more than your initial investment. You should not trade unless you fully understand the true extent of your exposure to the risk of loss. When trading, you must always take into consideration your level of experience. If the risks involved seem unclear to you, please seek independent financial advice.
